The Base Equation is the basis for the following equations used in the pressure loss calculations.  The pressure loss is expressed in psi or lbs/in² in the following equations.

Eq. (1)

Eq. (2)

     (Modified Zenz Equation)

Eq. (3)

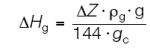Eq. (4)

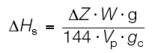Eq. (5)

= Estimated misc. losses from the systemÂ

Eq. (6)

The Fanning Friction Factor

In order to determine the fanning friction factor, f, the Reynolds Number must first be calculated:

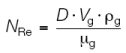
where ?_g is the gas viscosity in lbs/ft s.

Then, the friction factor is calculated from the following equation derived from pages A-23 and A-24 of Crane's Technical Paper No. 410:

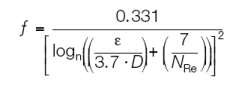
Where ? is the pipe roughness factor which can be estimated as 0.00015 for smooth pipes or 0.0005 for shot-peened pipes.

Pipe Equivalent Length

For straight pipe runs (either horizontal or vertical) use the actual length of the pipe.  For bends and other devices, use the table below as a guide:

Table 1: Equivalent Lengths in Conveying Systems

Component	Equivalent Length
Bends, 90° bend, long radius (10 to 1 radius to diameter ratio)	40 x diameter or 20 ft (whichever is larger)
Diverter Valves
45° divert angle	20 x diameter
30° divert angle	10 x diameter
Flexible Hoses
Stainless steel w/ lined interior	3 x pipe length
Rubber or vinyl hose	5 x pipe length
For bends that are less than 90°, use the following equivalent lengths: L =40 x (Degree of bend / 90)

Solids Velocity

Solids also move at a velocity lower than the gas velocity due to drag forces.  The difference between these velocities is called the slip factor.  For most course or hard solids, the slip factor is around 0.80. 

For fine powders, the solids velocity can be closer to the gas velocity and a factor of 0.90 may be more appropriate.  Depending on the size of the particles, the slip factor can range from 0.70 to 0.95.

Solids Velocity in Long Radius Bend

For a 90° radius bend, the solids velocity at the exit of the bend (V_p2) is around 0.80 times the solids velocity at the inlet of the bend (V_p1).  This factor can range from 0.60 to 0.90 depending of the properties of the solids.  For bends that are less than 90°, the exit velocity may be expressed as:

After leaving a 90° bend, use a nominal value of 20 pipe diameters for the length of pipe needed for the particles to accelerate back to their original velocity at the inlet of the bend.

Solids to Air Ratio

The solids to air ratio is calculated as:

In the above, m is the the solids mass flow in lb/s and A is the pipe cross sectional area in ft².  Remember that the gas density (and therefore velocity) will change throughout the system (we'll discuss this in more detail later).

When calculating the gas velocity, reduce the gas mass flow rate by 5% for pressure systems to account for gas leakage through a rotary valve if such a valve is used to feed the solids.

Gas Density and Pressure Loss

As the carrier gas moves through the system and losses or gains pressure (depending on whether the system is a pressure or vacuum system), it's density will increases or decrease accordingly thereby changing the velocity of the gas.   The gas pressure loss equation is shown in Equation 2 above.  The ideal gas law may be employed to calculate the density of the gas throughout the system.

Setting Up the Calculation

The method presented here can easily be set up in a spreadsheet to show the performance of your system.  It is recommend the divide the entire system into 5 to 10 ft sections for such a calculation.  The exit conditions of from section become the inlet conditions for the next and so on.  Also, be sure to account for any gas losses that are known and for any extra gas inlet points in the system.  For pressure systems, start from the end of the conveying line and return to the solids inlet point.  For vacuum systems, start from the solids inlet point and end at the blower inlet.

References

1. Zenz and Othmer, "Fluidized and Fluid Particle Systems", Chapters 10 and 11, published by Reinhold Publishing Corp, 1960
2. Agarwal, A.T., "Theory and Design of Dilute Phase Pneumatic Conveying Systems", Powder Handling & Processing, Vol. 17, No. 1, January/February 2005
3. Kimbel, Kirk W., "Troublefree Pneumatic Conveying", Chemical Engineering Magazine, April 1998, page 78