Chemical and Process Engineering Resources
Estimating Heat Capacities for Solutions with Dissolved Solids
Nov 08 2010 01:40 PM | Chris Haslego
Often times it is necessary to find the heat capacity for solutions with dissolved solids. A quick estimation method was proposed by Dimoplon in 1972.
The proposed expression is:
| Cp(soln) = W1 Cp(solid) + W2 Cp(water) | Eq. (1) |
where:
Cp(soln) = Heat capacity of the solution
Cp(solid) = Heat capacity of the dissolved solid
Cp(water) = Heat capacity of water
W1 = Weight percent of dissolved solid
W2 = Weight percent of water
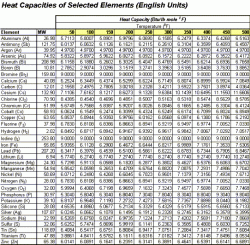
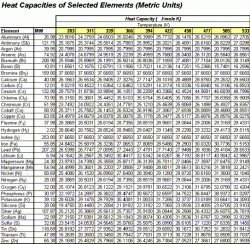
The following charts are used in the calculation to follow. Table 1 shows Engish units while Table 2 displays the values in Metric units.
| Table 1: Heat Capacity of Selected Element, English Units | Table 2: Heat Capacity of Selected Element, Metric Units |
 |  |
Step-by-Step Example
For an example problem, calculate the heat capacity of a 20% by weight solution of Na2CO3 at 150 °F.
Step 1
Look up the heat capacity of the solid or calculate this value from Kopp's Rule. If literature data is not available for the dissolved solid, it can be estimated from the elemental heat capacities with Kopp's Rule:
| Cp(Na2CO3) = 2 Cp(Na) + 1 Cp© + 3 Cp(O) | Eq. (2) |
From Table 1 above, we read the values at 150 °F. Notice that the heat capacity for oxygen is given as O2 (it's natural form). This value must be divided by two to get the heat capacity for one atom of oxygen.
Cp(Na2CO3) = 2 (6.8247) + 1 (2.7805) + 3 (1/2 (6.7198)) = 26.51 Btu/lb mole °F
Dividing by the molecular weight of the solid yields:
(26.51 Btu/lb mole °F) / (105.9 lb/lb mole) = 0.25 Btu/ lb °F
Step 2
Determine the heat capacity of the solution at a given temperature. Figure 1 below shows how the heat capacity of water varies with temperature in English units. To convert Btu/lb 0F to kJ/kg K, multiple by 4.1867.
Now, recall from Equation 1:
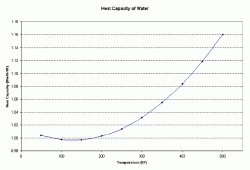 |
| Figure 1: Heat Capacity of Water as a Function of Temperature |
Cp(soln) = W1 Cp(solid) + W2 Cp(water)
Cp(soln) = 0.20 Cp(Na2CO3) + 0.80 Cp (water)
At 150 0F, the heat capacity of water is 0.9975 Btu/lb 0F.
Cp(soln) = 0.20 (0.25 Btu/lb 0F) + 0.80 (0.9975 Btu/lb 0F)
Cp(soln) = 0.848 Btu/lb 0F at 150 0F (literature data is 0.850)
Other Methods
A quick alternative to the above procedure was proposed by Vosseller in 1973:
Cp(soln) = 1 - 0.70 W1 (valid for English units only)
For the example shown here, the result would be 0.86 Btu/lb 0F
For aqueous organic solutions, Vosseller proposed:
Cp(soln) = 1 - 0.45 W1 (valid for English units only)
Download the MS Excel spreadsheet with the heat capacity data for the elements shown in Tables 1 and 2.

 FB
FB


1 Comments
Dear Mr. Haslego,
Can you help me with the Vosseller reference?.
I can´t find the information about his method.
Many Thanks.
Regards,
Napo.