Chemical and Process Engineering Resources
TankVolume, as it appears in the online store, calculates the liquid volume of partially filled tanks, horizontal or vertical, with various types of heads. One of these, the torispherical head, requires that integral equations be solved. This article shows how the integrals are evaluated.
Torispherical heads are made up of two parts. The rounded end has a spherical shape. It has a radius that is described with the numerical value “f†which is the ratio of the dish radius to the vessel shell diameter.
Torispherical heads are also called “F&D†or “flanged and dishedâ€. The standard F&D head has f = 1.0 and kD = 3 times the metal thickness of the head. ASME F&D heads require a dish radius no greater than the diameter (f <= 1.0) and knuckle radius no less than 6% of the diameter (k >= 0.06) or three times the metal thickness, whichever is greater.
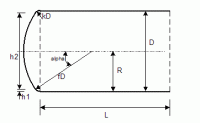 |
Figure 1: Torispherical Head |
When calculating the volume of fluid in a torispherical head, the head is divided into three parts. The first is the lower portion occupied by the knuckle (liquid height 0 to h1 as seen in the diagram). The second part is the portion covered by the spherical dish section, which also includes the knuckle at the perimeter. The third portion is that which is entirely within the knuckle but above the spherical section.
Each of the three parts are calculated separately and they each require solving an integral. I’ll use the integral for the first part for an example in this article.
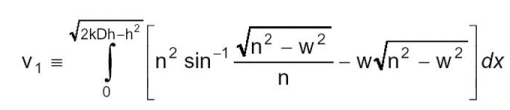 | Eq. (1) |
where
           k = knuckle radius
           D = vessel diameter
           h = fill height of the vessel
           n = R – kD + (k2D2 – x2)^0.5, where R = vessel radius (= D/2)
           w = R – h
It looks complicated, but solving in Excel is straightforward if it is done sequentially as described below.
Integrals that are too complex to express implicitly are solved using “numerical methodsâ€. A number of numerical methods have been used for integrals with Simpson’s Rule being one of the best. I chose to use Simpson’s Rule for this problem. (Other methods include the trapezoidal rule, Riemann sums, Romberg integration, Gaussian quadratures and the Monte Carlo method). There are many webpages that give the derivation of Simpson’s Rule and explain it in detail; I won’t repeat that work here.
Simpson’s rule requires that the integral be broken into intervals. Since the integral is evaluating the area under a curve, from x=0 to x= (2kDh-h2)^.5, the method first calculates the maximum value for x, divides that by the number of intervals, and then evaluates the function for each value of x. In other words, if the maximum value of x was 10 and there were 10 intervals, then the function would be evaluated with x = 0, 1, 2, 3, 4, etc.  Notice that the term called “n†above includes x in its formula.
An even number of intervals is required. The more the better.  I found through trial and error that a good number to use for this particular problem is 1000 intervals.
Implementation could be done in a tabular form on an Excel worksheet. However, it is much more elegant to solve Simpson’s Rule in a Visual Basic for Applications function subroutine.  Listing 1 gives the function. This is located in a VBA Module within TankVolume. Each place the calculation is required, the function is called using a cell formula of the form:
= Toris_V1(k, D, h)
where the variables k, D, and h are as defined above. Since recalculation takes time, which can be noticable, I put the function call in a conditional statement so it is only used when the tank is horizontal with torispherical heads. Assume the variable “head_type†refers to the type of head and a value of head_type=4 refers to torispherical, the conditional function call becomes:
= if(head_type=4,Toris_V1(k, D, h), 0)
In this case, the function is called only if the heads are torispherical. Otherwise, a value of “0†is returned. This is perfectly fine since the result of this cell in the spreadsheet is only used for torispherical heads.
| Function Toris_V1(k, D, H) As Double ' ' Integral solution using Simpson's Rule ' Dim interval As Double Dim i As Integer Dim n As Double, n1 As Double, n2 As Double Dim X As Double, xmax As Double Dim steps As Integer Dim func As Double, sumfunc As Double ' On Error GoTo err_TorisV1 steps = 1000 ' '----------------------------------------------------------- ' Procedure: ' evaluate the maximum value for x (minimum value=0) ' for each value of x from min to max, at each interval, '  calculate n '  calculate the function '  sum results according to Simpson's Rule ' calculate result and return ' ' Derived function (arcsin is not an intrinsic function) '   Arcsin(x) = Atn (x / Sqr(-x * x + 1)) '----------------------------------------------------------- ' ' maximum value of x xmax = (2 * k * D * H - H ^ 2) ^ 0.5 R = D / 2 w = R - H interval = xmax / steps sumfunc = 0 X = 0 n1 = R - k * D n2 = k ^ 2 * D ^ 2 For i = 0 To steps    n = n1 + Sqr(n2 - X ^ 2)    func = Sqr(n ^ 2 - w ^ 2) / n    func = n ^ 2 * Atn(func / Sqr(-func * func + 1)) - w * Sqr(n ^ 2 - w ^ 2)    sumfunc = sumfunc + func    If i > 0 And i < steps Then        If (i / 2) = Int(i / 2) Then sumfunc = sumfunc + func Else sumfunc = sumfunc + 3 * func    End If    X = X + interval    If X > xmax Then X = xmax Next i ' Toris_V1 = sumfunc * interval / 3 Exit Function ' err_TorisV1: Toris_V1 = 0 ' End Function |

 FB
FB


2 Comments