Chemical and Process Engineering Resources
Analysis One
This analysis derives the relationship between the stagnation temperature, flowing temperature, and the Mach number for a flowing ideal gas. Stagnation temperature is the temperature a flowing gas rises to when it is brought isentropically to rest, thereby converting its kinetic energy into enthalpy.
Conservation of energy requires that the energy balances:
 | Eq. (1) |
For adiabatic flow, no shaft work and for gases: Q=0, Ws=0 and dz=negligible....or:
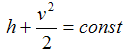 | Eq. (2) |
Enthalpy per unit mass of an ideal gas is defined H = Cp T
The gas, at rest, has no kinetic energy and is at its stagnation temperature (Tst), while the moving gas has kinetic energy and is at another temperature (T). The energies are therefore:
energy at rest, per unit mass = 0 + Cp Tst
energy in motion, per unit mass = v2/2 + Cp T
Equating the energy at rest and in motion:
| hst= h+v2/2 | Eq. (3) |
or
| h= hst-v2/2 | Eq. (4) |
or
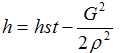 | Eq. (5) |
This implies:
- Stagnation enthalpy of the fluid during adiabatic flow is constant. For an ideal gas, this implies the stagnation temperature is constant.
- Enthalpy of the gas drops and kinetic energy increases in the direction of flow.
- For as given mass flux the enthalpy and density are related to each other.
A useful way of looking at this relationship is by fanno lines. The fanno lines are lines of constant mass flux plotted on an enthalpy/entropy diagram:
 |
| Figure 1: Sub-sonic Flanno Flow |
| Cp Tst = v2/2 + Cp T | Eq. (6) |
To make this equation useful, we must replace Cp and v by terms containing only constants and the Mach number.
Also for an ideal gas:
 | Eq. (7) |
and
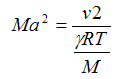 | Eq. (8) |
Substituting yields:
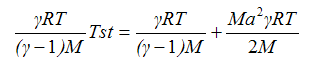 | Eq. (9) |
or
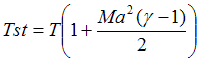 | Eq. (10) |
Thus we see that for an ideal gas the temperature decreases as velocity increases.
If the gas is flowing adiabatically, then no energy has been added or subtracted from it and Tst is constant along the length of the pipe. Knowing Tst, then the above equation can be used to find the flowing temperature from the Mach number, (or vice versa) at any position along the pipe.

 FB
FB



0 Comments