Analysis Two

This analysis uses the principles of conservation of energy and mass to derive a relationship between pressure and Mach number at up and downstream conditions, for adiabatic flow in a pipe of constant cross-sectional area.

The conservation of mass requires the mass flux to be the same at any position along a pipe. Mass flux at any of these positions can be expressed in terms of density and velocity :

Eq. (11)

For an ideal gas:

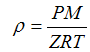Eq. (12)

and

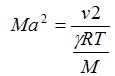Eq. (13)

Substituting for density and velocity, we obtain Equation14 which relates Mach number, mass flow rate and flowing pressure and temperature:

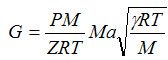Eq. (14)

or

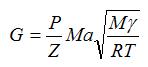Eq. (15)

Substituting for T from Equation 10:

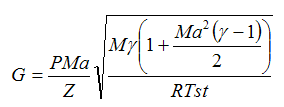Eq. (16)

G is same at inlet (1) and outlet(2), so:

 

Eq. (17)

which leads to:

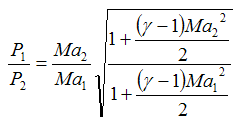Eq. (18)

This implies that pressure decreases as the Mach number increases. A similar analysis for temperature gives:

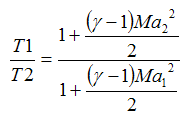Eq. (19)

This implies that temperature decreases as the Mach number increases. However, this is true for ideal gases only. For real gases temperature may increase!

Analysis Three

Now the momentum equation is introduced to incorporates the losses due to friction. The derivation is available in any standard textbook for compressible flow In summary the final result is:

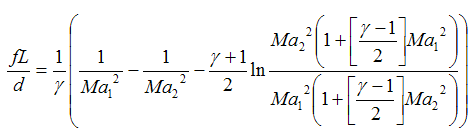Eq. (20)

where

f= Average Darcy friction factor
L= Equivalent length of line
d= I.D. of the line

Thus this equation relates losses due to friction to inlet and outlet velocities. Solving for the unknown parameter requires a trial and error approach and is suitable for an Excel spreadsheet using the "Goal Seek" or "Solver" tools. Depending on the number of unknowns one or all three of the following equations need to be solved simultaneously:

Mass balance Equation 11
Energy balance Equation18 or 19
Momentum balance Equation 20.

In cases where the outlet velocity is defined as Mach 1, then the equation can be solved for the maximum length, which can be used to flow a certain amount of fluid through a line of known diameter. Beyond this length choked flow condition occurs and, as explained above, any further increase in pipe length will cause the flow to decrease in such a manner that velocity at the end of the pipe is still sonic ( Mach=1). This particular application is of considerable practical use in sizing blowdown lines or relief valve outlet lines relieving to the atmosphere.

Recall that the above equations have assumed that the gas is ideal. One can compensate for non-ideality to an extent by incorporating the Z factor. A rigorous approach implies solving simultaneously the momentum, energy, and mass balance equation numerically. An analytical approach, as given above for ideal gases, is useful most of the time and the results are valid for engineering purpose.

Isothermal Flow

In isothermal flow, the temperature of the gas remains constant. This simplifies matters considerably. Starting with the mechanical energy equation:

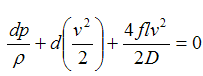Eq. (21)

Multiplying both sides by ?²:

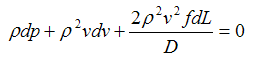Eq. (22)

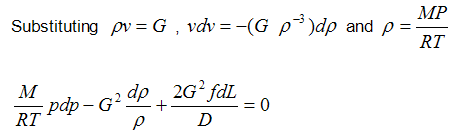Eq. (23)

Rearranging and integrating gives:

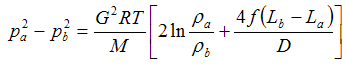Eq. (24)

When the temperature change over the conduit is small Equation 24 can be used instead of the adiabatic Equation 20.  Adibatic flow below Mach 0.3 follows Equation 24 closely.

If Equation 24 is differentiated with respect to ?_b   to obtain a maximum G then:

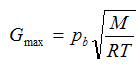Eq. (25)

and the exit Mach number is:

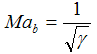Eq. (26)

This apparent choking condition for isothermal flow is not physically meaningful, as at these high speeds, and rates of expansion, isothermal conditions are not possible.

References

1. Unit operations of Chemical Engineering- Mccabe, Smith and Hariott; McGraw-Hill
2. Perry's Chemical Engineers' Handbook' McGraw-Hill.