Relationship Between K, Friction Factor, and Equivalent Length

The following discussion is based on concepts found in reference 1, the CRANE Technical Paper No. 410. It is the author's opinion that this manual is the closest thing the industry has to a standard on performing various piping calculations. If the reader currently does not own this manual, it is highly recommended that it be obtained.

As in straight pipe, velocity increases through valves and fittings at the expense of head loss. This can be expressed by another form of the Darcy equation similar to Equation 1:

Eq. (3)

When comparing Equations 1 and 3, it becomes apparent that:

Eq. (4)

K is called the resistance coefficient and is defined as the number of velocity heads lost due to the valve or fitting. It is a measure of the following pressure losses in a valve or fitting:

• Pipe friction in the inlet and outlet straight portions of the valve or fitting
• Changes in direction of flow path
• Obstructions in the flow path
• Sudden or gradual changes in the cross-section and shape of the flow path

Pipe friction in the inlet and outlet straight portions of the valve or fitting is very small when compared to the other three. Since friction factor and Reynolds Number are mainly related to pipe friction, K can be considered to be independent of both friction factor and Reynolds Number. Therefore, K is treated as a constant for any given valve or fitting under all flow conditions, including laminar flow. Indeed, experiments showed¹ that for a given valve or fitting type, the tendency is for K to vary only with valve or fitting size. Note that this is also true for the friction factor in straight clean commercial steel pipe as long as flow conditions are in the fully developed turbulent zone. It was also found that the ratio L/D tends towards a constant for all sizes of a given valve or fitting type at the same flow conditions. The ratio L/D is defined as the equivalent length of the valve or fitting in pipe diameters and L is the equivalent length itself.

In Equation 4, f therefore varies only with valve and fitting size and is independent of Reynolds Number. This only occurs if the fluid flow is in the zone of complete turbulence (see the Moody Chart in reference 1 or in any textbook on fluid flow). Consequently, f in Equation 4 is not the same f as in the Darcy equation for straight pipe, which is a function of Reynolds Number. For valves and fittings, f is the friction factor in the zone of complete turbulence and is designated f_t, and the equivalent length of the valve or fitting is designated L_eq. Equation 4 should now read (with D being the diameter of the valve or fitting):

Eq. (5)

The equivalent length, L_eq, is related to f_t, not f, the friction factor of the flowing fluid in the pipe. Going back to step four in our five step procedure for calculating the total pressure drop in the pipe, adding the equivalent length to the straight pipe length for use in Equation 1 is fundamentally wrong.

Calculating Pressure Drop, The Correct Way

So how should we use equivalent lengths to get the pressure drop contribution of the valve or fitting? A form of Equation 1 can be used if we substitute f_t for f and L_eq for L (with d being the diameter of the valve or fitting):

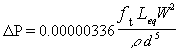Eq. (6)

The pressure drop for the valves and fittings is then added to the pressure drop for the straight pipe to give the total pipe pressure drop.

Another approach would be to use the K values of the individual valves and fittings. The quantity of each type of valve and fitting is multiplied by its respective K value and added together to obtain a total K. This total K is then substituted into the following equation:

Eq. (7)

Notice that use of equivalent length and friction factor in the pressure drop equation is eliminated, although both are still required to calculate the values of K¹. As a matter of fact, there is nothing stopping the engineer from converting the straight pipe length into a K value and adding this to the K values for the valves and fittings before using Equation 7. This is accomplished by using Equation 4, where D is the pipe diameter and f is the pipeline friction factor.

How significant is the error caused by mismatching friction factors? The answer is, it depends. Below is a real world example showing the difference between the Equivalent Length method (as applied by most engineers) and the K value method to calculate pressure drop.