Chemical and Process Engineering Resources

Conventional Jackets
 |
| Figure 1: Conventional Jacket |
"Conventional jackets" can be divided into two (2) main categories: baffled and non-baffled. Baffled jackets often utilize what is known as a spirally wound baffle. The baffle consist of a metal strip wound around the inner vessel wall from the jacket utility inlet to the utility outlet. The baffle directs the flow in a spiral path with a fluid velocity of 1-4 ft/s. The fabrication methods does allow for small internal leakage or bypass around the baffle. Generally, bypass flows can exceed 1/3 to 1/2 of the total circulating flow.
Conventional baffled jackets are usually applied with small vessels using high temperatures where the internal pressure in more than twice the jacket pressure.
Spirally baffled jackets are limited to a pressure of 100 psig because vessel wall thickness becomes large and the heat transfer is greatly reduced. In the case of an alloy reactor, a very costly vessel can result. For high temperature applications, the thermal expansion differential must be considered when choosing materials for the vessel and jacket. Design and construction details are given in Division 1 of the ASME Code, Section VIII, Appendix IX, "Jacketed Vessel".
Heat Transfer Coefficients: Conventional Jackets without Baffles
| (hj De / k) = 1.02 (NRe) 0.45 (NPr) 0.33 (De/ L) 0.4 (Djo/ Dji) 0.8 (NGr) 0.05 | Eq. (1) |
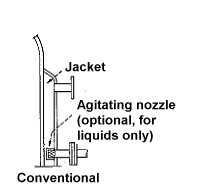 |
| Figure 2: Schematic of Conventional Jacket |
Where:
hj = Local heat transfer coefficient on the jacket side
De = Equivalent hydraulic diameter
NRe = Reynolds Number
NPr = Prandtl Number
L = Length of jacket passage
Djo = Outer diameter of jacket
Dji = Inner diameter of jacket
NGr = Graetz number
NRe = DVρ/μ
Where D is the equivalent diameter, V is the fluid velocity, ρ is the fluid density, μ and is the fluid viscosity.
The Prandtl Number is defined as:
NPr = Cp μ / k
Where Cp is the specific heat, μ is the viscosity, and k is the thermal conducitivity of the fluid.
The Graetz Number is defined as:
NGr = (m Cp) / (k L)
Where m is the mass flow rate, Cp is the specific heat, k is the thermal conducitivity, and L is the jacket passage length.
The equivalent diameter is defined as follows:
De = Djo-Dji for laminar flow
De = ((Djo)2 - (Dji)2)/Dji for turbulent flow
Conventional Jackets with Baffles
For conventional jackets with baffles, the following can be used to calculate the heat transfer coefficient:
| hj De/k= 0.027(NRe)0.8 (NPr)0.33 (µ/µw)0.14 (1+3.5 (De/Dc) ) ( For NRe > 10,000) | Eq. (2) |
| hj De/k = 1.86 [ (NRe) (NPr) (Dc/De) ] 0.33 (µ/µw)0.14 ( For NRe < 2100 ) | Eq. (3) |
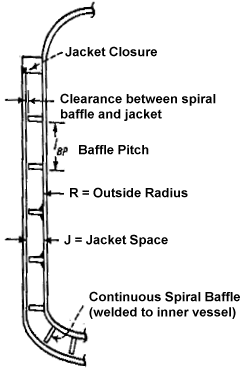 |
Figure 3: Schematic of Conventional Jacket |
Two new variables are introduced. Dc is defined as the centerline diameter of the jacket passage. It is calculated as Dji + ((Djo-Dji)/2). The viscosity at the jacket wall is now defined as µw. When calculating the heat transfer cofficients, an effective mass flow rate should be taken as 0.60 x feed mass flow rate to account for the substantial bypassing that will be expected. De is defined at 4 x jacket spacing. The flow cross sectional area is defined as the baffle pitch x jacket spacing.
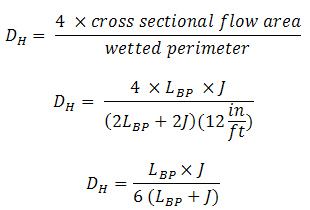 | Eq. (4)
Eq. (5)
Eq. (6) |

 FB
FB

2 Comments
Very useful guidance for designing Jacketed vessel. Thank you for your sharing.
thank you, but i have an situation here i already fabricated double jacket tank half pipe but i need another type of jacket to prevent marks of welding on the inner tank walls. kindly see below picture
http://postimg.org/image/4xhiuehkn/
http://postimg.org/image/ctl1tbqt3/
http://postimg.org/image/5cgfruqnr/
cloud you please advise