Chemical and Process Engineering Resources
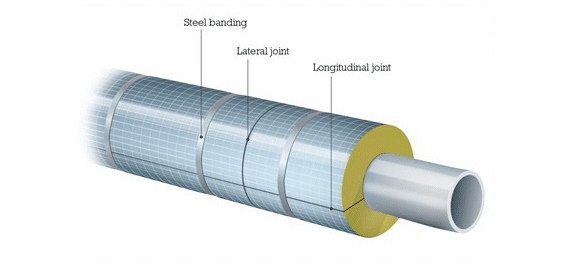
Safety
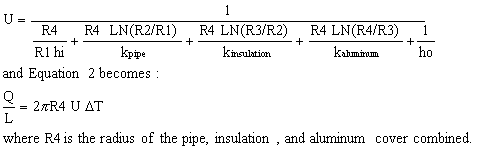 | Eq. (3) |
However, when considering safety, engineers need a quick way to calculate the surface temperature that will come into contact with the workers. This can be done with equations or the use of charts. We start by looking at another diagram:
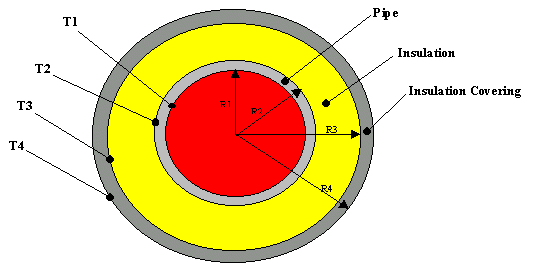
At steady state, the heat transfer rate will be the same for each layer:
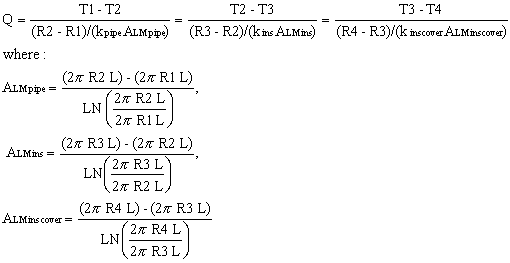 | Eq. (4) |
Rearranging Equation 4 by solving the three expressions for the temperature difference yields:
 | Eq. (5) |
Each term in the denominator of Equation 5 is referred to as the "resistance" of each layer. We will define this as Rs and rewrite the equation as:
| Eq. (6) |
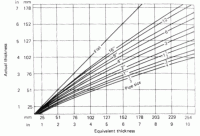 |
| Figure 4: Equivalent Thickness Chart for Calcium Silicate Insulation |
Since the heat loss is constant for each layer, use Equation 4 to calculate Q from the bare pipe, then solve Equation 6 for T4 (surface temperature). Use the economic thickness of your insulation as a basis for your calculation, after all, if the most affordable layer of insulation is safe, that's the one you'd want to use. If the economic thickness results in too high a surface temperature, repeat the calculation by increasing the insulation thickness by 1/2 inch each time until a safe touch temperature is reached.
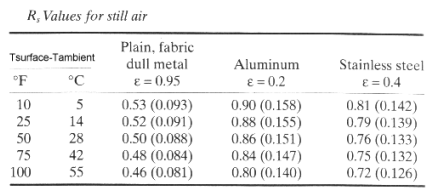
As you can see, using heat balance equations is certainly a valid means of estimating surface temperatures, but it may not always be the fastest. Charts are available that utilize a characteristic called "equivalent thickness" to simplify the heat balance equations. This correlation also uses the surface resistance of the outer covering of the pipe. Figure 4 shows the equivalent thickness chart for calcium silicate insulation. Table 5 shows surface resistances for three popular covering materials for insulation.
 |
With the help of Figure 4 and Table 5 (or similar data for another material you may be dealing with), the relation:
| Eq. (7) |
can be used to easily determine how much insulation will be needed to achieve a specific surface temperature. Let's look at an example to illustrate the various uses of this equation.
Example of Outer Surface Temperature Determination
Your supervisor asks you to install insulation on a new pipe in the plant. Recently, two workers suffered severe burns while incidentally touching the new piping so safety is of primary concern. He instructs you to be sure that this incident does not repeat itself. The pipe contains a heat transfer fluid at 850 °F (454 °C). The ambient temperature is usually near 85 °F (29.4 °C). After checking the supplies that you have available, you notice that you have calcium silicate insulation and aluminum available for covering. You would like to insulate the 16 inch pipe for a surface temperature of 130 °F.
![]()
Tsurface - Tambient = 130 °F - 85 °F = 45 °F, from Table 5 we estimate a Rs value for aluminum at 0.865 h ft2 °F/Btu.
Taverage = (850 °F + 85 °F)/2 = 467.5 °F (242 °C), from Figure 1 we estimate a thermal conductivity of 0.0365 Btu/h ft °F (0.06317 W/m °C) for calcium silicate insulation.
![]()
From Figure 4 above, an equivalent thickness of 6 in corresponds to an actual thickness of nearly 5.0 in of insulation.

 FB
FB


2 Comments
Great article and very helpful.