Chemical and Process Engineering Resources
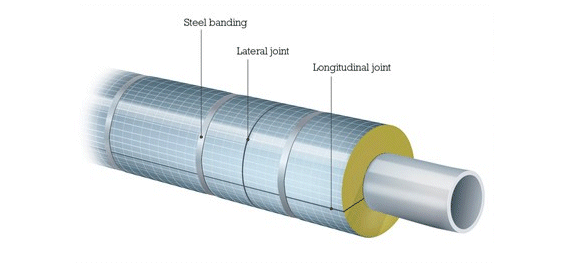
Process Conditions
The temperature of a fluid inside an insulated pipe is an important process variable that must be considered in many situations. Consider the length of pipe connecting two pieces of process equipment shown below:
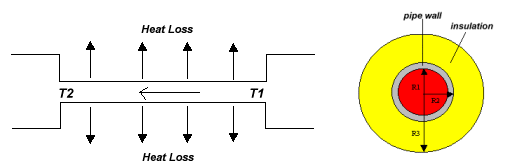
In order to predict T2 for a given insulation thickness, we first make the following assumptions:
- Constant fluid heat capacity over the fluid temperature range
- Constant ambient temperature
- Constant thermal conductivity for fluid, pipe, and insulation
- Constant overall heat transfer coefficient
- Turbulent flow inside pipe
- 15 mph wind for outdoor calculations
![]()
where
 | Eq. (8) |
and another heat balance equation yields:
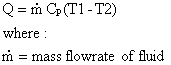 | Eq. (9) |
Setting Equation 8 equal to Equation 9 and solving for T2 yields:
| Eq. (10) |
Equation 10 provides another useful tool for analyzing insulation and its impact on a process. Equation 10 has been incorporated into the "Insulated Pipe Temperature Prediction Spreadsheet" available in the Download Section.
One example may be the importance of designing insulation thickness to prevent condensation on cold lines. Usually, when we hear the word "insulation" we instantly think of hot lines. However, there are times when insulation is used to prevent heat from entering a line. In this situation, the dew point temperature of the ambient air must be considered. Table 6 and Table 7 show dewpoint temperatures as a function of relative humidity and dry bulb temperatures.
| Table 6: Dew Point Temperatures of Air (Fahrenheit) | Table 7: Dew Point Temperatures of Air (Celsius) | |
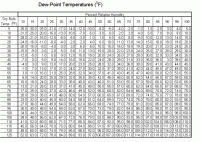 |  |
It is crucial that sufficient insulation is added so that the outer temperature of the insulation remains above the dewpoint temperature. At the dewpoint temperature, moisture in the air will condense onto the insulation and essentially ruin it.
Special Case
For the case of a bare pipe running outside, the chart below can be used to adjust the external heat transfer coefficient from 50 W/m2 K (8.8 Btu/h ft2 °F) to account for temperature difference and wind velocity:
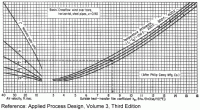 |
| Figure 6: Bare Pipe External Heat Transfer Coefficient Adjustment |
Practical Example
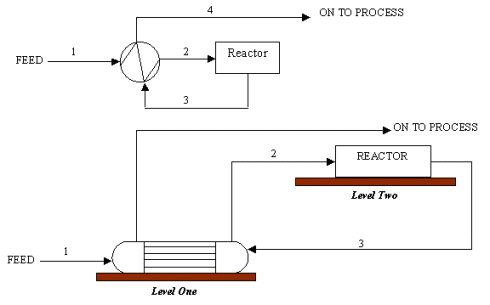
Data:
Calcium silicate insulation
Temperature of stream 2 exiting the heat exchanger is 400 °C (752 °F)
Ambient temperature is 23.8 °C (75 °F)
Mass flow = 350,000 kg/h (771,470 lbs/h)
Rinside pipe = R1 = 101.6 mm (4.0 in)
Routside pipe = R2 = 108.0 mm (4.25 in)
Thermal conductivity of pipe = kpipe = 30 W/m K (56.2 Btu/h ft °F)
Ambient air heat transfer coefficient = ho = 50 W/m2 K (8.8 Btu/h ft2 °F)
Fluid heat capacity = Cpfluid = 2.57 kJ/kg K (2.0 Btu/lb °F)
Fluid thermal conductivity = kfluid = 0.60 W/m K (1.12 Btu/h ft °F)
Fluid viscosity = ufluid = 5.2 cP
Energy costs = $4.74/million kJ ($5.00/million Btu)
Equivalent length of pipe = 100 meters (328 feet)
Calculations: Temperature difference with insulation is 3.56 0C. While this doesn't sound too dramatic, consider the energy savings over one year with the insulation: Q = mass flow x Cpfluid x temperature difference By insulating the pipe, energy costs have decreased by nearly $133,000 per year Summary There are many factors to consider when thinking about insulation. Insulation save money for certain, but it can also be effective as a safety and process control device. Insulation can be used to regulate process temperatures, protect workers from serious injury, and save thousands of dollars in energy costs. One should never overlook it's usefulness. It's also bad practice to consider only one of the important factors discussed in this article. The key is to consider all factors that will be affected by installing insulation on a pipe or any other piece of equipment.
First, we'll assume little or no wind affects the pipe heat loss and we'll estimate the heat loss from the bare pipe:
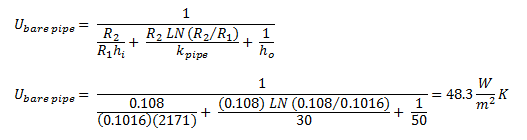
Now, we'll estimate the radiant heat losses:
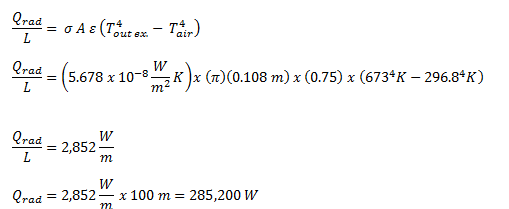
where:
σ = Stefan-Boltzmann constant = 5.678 x 10-8 W/m2 K
A = circumference of pipe to the outer diameter, m
ε = emissivity of pipe material, taken at 673 K, assume 0.75
T = absolute temperatures, K
Now, we'll estimate the losses due to convection:
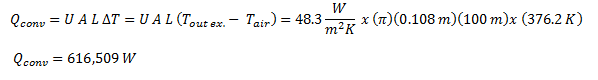
and we'll add these together to arrive at the total heat loss for the bare pipe:
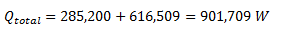
We can now calculate the temperature entering the reactor from the heat exchanger for the bare pipe scenario:
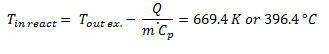
Now, we perform a similar analysis for the insulated pipe:

Q = (350,000 kg/h)(2.57 kJ/kg K)(3.56 K) = 3,202,220 kJ/h
3,202,220 kJ/h x 8760 hours/year = 28,051 million kJ/year
28,051 million kJ/year x $4.74/million kJ = $132,961 per year
Heat Transfer Articles

 FB
FB


2 Comments
Great article and very helpful.