Step 7: Estimation of the Optimum DTmin Value by Energy-Capital Trade Off

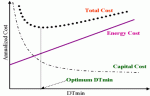Figure 9: Energy-Capital Cost Trade Off (Optimum DTmin)

To arrive at an optimum DTmin value, the total annual cost (the sum of total annual energy and capital cost) is plotted at varying DTmin values (Figure 7). Three key observations can be made from Figure 9:

1. An increase in DTmin values result in higher energy costs and lower capital costs.
2. A decrease in DTmin values result in lower energy costs and higher capital costs.
3. An optimum DTmin exists where the total annual cost of energy and capital costs is minimized.

Thus, by systematically varying the temperature approach we can determine the optimum heat recovery level or the DT_minOPTIMUM for the process.

Step 8: Estimation of Practical Targets for HEN Design

The heat exchanger network designed on the basis of the estimated optimum DTmin value is not always the most appropriate design. A very small DTmin value, perhaps 8 0C, can lead to a very complicated network design with a large total area due to low driving forces. The designer, in practice, selects a higher value (15 °C) and calculates the marginal increases in utility duties and area requirements. If the marginal cost increase is small, the higher value of DTmin is selected as the practical pinch point for the HEN design.

Recognizing the significance of the pinch temperature allows energy targets to be realized by design of appropriate heat recovery network.

So what is the signficance of the pinch temperature?

The pinch divides the process into two separate systems each of which is in enthalpy balance with the utility. The pinch point is unique for each process. Above the pinch, only the hot utility is required. Below the pinch, only the cold utility is required. Hence, for an optimum design, no heat should be transferred across the pinch. This is known as the key concept in Pinch Technology.

To summarize, Pinch Technology gives three rules that form the basis for practical network design:

• No external heating below the Pinch.
• No external cooling above the Pinch.
• No heat transfer across the Pinch.

Violation of any of the above rules results in higher energy requirements than the minimum requirements theoretically possible.

The Plus/Minus Principle

The overall energy needs of a process can be further reduced by introducing process changes (changes in the process heat and material balance). There are several parameters that could be changed such as reactor conversions, distillation column operating pressures and reflux ratios, feed vaporization pressures, or pump-around flow rates. The number of possible process changes is nearly infinite. By applying the pinch rules as discussed above, it is possible to identify changes in the appropriate process parameter that will have a favorable impact on energy consumption. This is called the "Plus/Minus Principle."

Applying the pinch rules to study of composite curves provide us the following guidelines:

• Increase (+) in hot stream duty above the pinch.
• Decrease (-) in cold stream duty above the pinch.

This will result in a reduced hot utility target, and any

• Decrease (-) in hot stream duty below the pinch.
• Increase (+) in cold stream duty below the pinch

will result in a reduced cold utility target.

These simple guidelines provide a definite reference for the adjustment of single heat duties such as vaporization of a recycle, pump-around condensing duty, and others. Often it is possible to change temperatures rather than the heat duties. The target should be to

• Shift hot streams from below the pinch to above and
• Shift cold streams from above the pinch to below.

The process changes that can help achieve such stream shifts essentially involve changes in following operating parameters:

• reactor pressure/temperatures
• distillation column temperatures, reflux ratios, feed conditions, pump around conditions, intermediate condensers
• evaporator pressures
• storage vessel temperatures

For example, if the pressure for a feed vaporizer is lowered, vaporization duty can shift from above to below the pinch. The leads to reduction in both hot and cold utilities.

Appropriate Placement Principles

Apart from the changes in process parameters, proper integration of key equipment in process with respect to the pinch point should also be considered. The pinch concept of "Appropriate Placement" (integration of operations in such a way that there is reduction in the utility requirement of the combined system) is used for this purpose. Appropriate placement principles have been developed for distillation columns, evaporators, heat engines, furnaces, and heat pumps. For example, a single-effect evaporator having equal vaporization and condensation loads, should be placed such that both loads balance each other and the evaporator can be operated without any utility costs. This means that appropriate placement of the evaporator is on either side of the pinch and not across the pinch.

In addition to the above pinch rules and principles, a large number of factors must also be considered during the design of heat recovery networks. The most important are operating cost, capital cost, safety, operability, future requirements, and plant operating integrity. Operating costs are dependent on hot and cold utility requirements as well as pumping and compressor costs. The capital cost of a network is dependent on a number of factors including the number of heat exchangers, heat transfer areas, materials of construction, piping, and the cost of supporting foundations and structures.

With a little practice, the above principles enable the designer to quickly pan through 40-50 possible modifications and choose 3 or 4 that will lead to the best overall cost effects.

The essence of the pinch approach is to explore the options of modifying the core process design, heat exchangers, and utility systems with the ultimate goal of reducing the energy and/or capital cost.

Step 9: Design of the Heat Exchanger Network

The design of a new HEN is best executed using the "Pinch Design Method (PDM)". The systematic application of the PDM allows the design of a good network that achieves the energy targets within practical limits. The method incorporates two fundamentally important features: (1) it recognizes that the pinch region is the most constrained part of the problem (consequently it starts the design at the pinch and develops by moving away) and (2) it allows the designer to choose between match options.

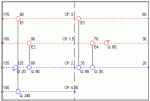Figure 10: Typical Grid Diagram

In effect, the design of network examines which "hot" streams can be matched to "cold" streams via heat recovery. This can be achieved by employing "tick off" heuristics to identify the heat loads on the pinch exchanger. Every match brings one stream to it target temperature. As the pinch divides the heat exchange system into two thermally independent regions, HENs for both above and below pinch regions are designed separately. When the heat recovery is maximized the remaining thermal needs must be supplied by hot utility.

The graphical method of representing flow streams and heat recovery matches is called a ‘grid diagram’ (Figure 10).

All the cold (blue lines) and hot (red line) streams are represented by horizontal lines. The entrance and exit temperatures are shown at either end. The vertical line in the middle represents the pinch temperature. The circles represent heat exchangers. Unconnected circles represent exchangers using utility heating and cooling.

The design of a network is based on certain guidelines like the "CP Inequality Rule", "Stream Splitting", "Driving Force Plot" and "Remaining Problem Analysis". The stepwise procedure can be understood better with the help of an example problem.

Having made all the possible matches, the two designs above and below the pinch are then brought together and usually refined to further minimize the capital cost. After the network has been designed according to the pinch rules, it can be further subjected to energy optimization. Optimizing the network involves both topological and parametric changes of the initial design in order to minimize the total cost.