Methods of Estimating Physical Properties

When specifying a liquid-liquid heat exchanger, the specifying engineer must be able to provide physical properties that are as accurate as possible. For liquid-liquid duties, the following data should be provided for each fluid: density, thermal conductivity, specific heat (sometimes called heat capacity), and viscosity. Ideally, these properties should be provided for each fluid at both the inlet and outlet temperature of the exchanger.

If data is limited, there are some estimating rules that be of assistance. The physical properties that will impact the design of the exchangers the most are the viscosity and the specific heat. Recall that the specific heat of a fluid is required in order to accurately specify the exchanger. Now, we'll examine estimation methods for each of the physical properties. While actual plant data or experimentally determined data is preferred, these methods can be used when no other data is available. For our estimation methods, we'll assume that typical process fluids are made up of mixtures of components and that the data for each component is available. This is almost always the case.

Specific Heat

For fluid mixtures where there is no known heat of mixing, a weighted average can be used:

Eq. (8)

Where:

C_pmix = Heat capacity of the mixture in consistent units
W₁ = Weight fraction of component one
C_pL1 = Heat capacity of component one in consistent units
W₂ = Weight fraction of component two
C_pL2 = Heat capacity of component two in consistent units

If using the above method, look up the heat capacity of the components at the average temperature through the heat exchanger. It's not uncommon to provide heat exchanger designers with a single heat capacity point for each fluid. Be aware that the heat capacity of most liquids will increase with temperature.

Viscosity

While it's not critical to supply a physical property point at the inlet and outlet temperature for other properties, it's very beneficial to do for the viscosity of the fluids. Using only a single viscosity point will affect both the heat transfer and pressure drop calculation of any heat exchanger.

For non-polar mixtures, the following has shown to provide viscosity estimates to within +/- 5 -10%:

Eq. (9)

Where:

µ_mix = Viscosity of mixture in centipoise
W₁ = Weight fraction of component one
µ₁ = Viscosity of component one in centipoise
W₂ = Weight fraction of component two
µ₂ = Viscosity of component two in centipoises

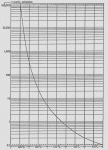Figure 8: Viscosity Correlation Chart

For polar fluids, electrolyte solutions, and non-newtonian fluids, it is highly advisable to either find reliable data or have an outside lab perform testing. There is an estimation method available for polar mixtures called the "Method of Grunberg and Nissan". This method is detailed in Properties of Liquids and Gases, Edition 4 by Reid et al. (ISBN 0070517991, see page 474).

If viscosity data is available at one temperature, the following correlation chart (Figure 8) that has been used for years to estimate the viscosity at a second temperature. This chart is used by finding the single available viscosity point on the Y-axis and move left to meet the curve. Then, on the X-axis, adjust the temperature difference up or down by the temperature change required. Next, move up to hit the curve again and read the resulting viscosity from the Y-axis.

Thermal Conductivity

The thermal conductivities of mixtures can be estimated via the same weighted average method shown in Equation 9 for specific heat calculations. The calculation is the same, just replace the component specific heats with the component thermal conductivities. In cases where there is a complete absence of data, keep the following ranges in mind:

Water based mixtures, thermal conductivity range is about 0.28 to 0.35 Btu/ h ft °F

Hydrocarbon based mixtures, thermal conductivity range is about 0.055 to 0.080 Btu/ h ft °F

Density

The density of mixtures represents another case where a weighted average method is usually adequate as an estimate for heat exchanger design.