This is the statement of the problema I've invented (I studied McCabe-Thiele in spanish, so maybe there's somethings that are not well written, sorry for that):
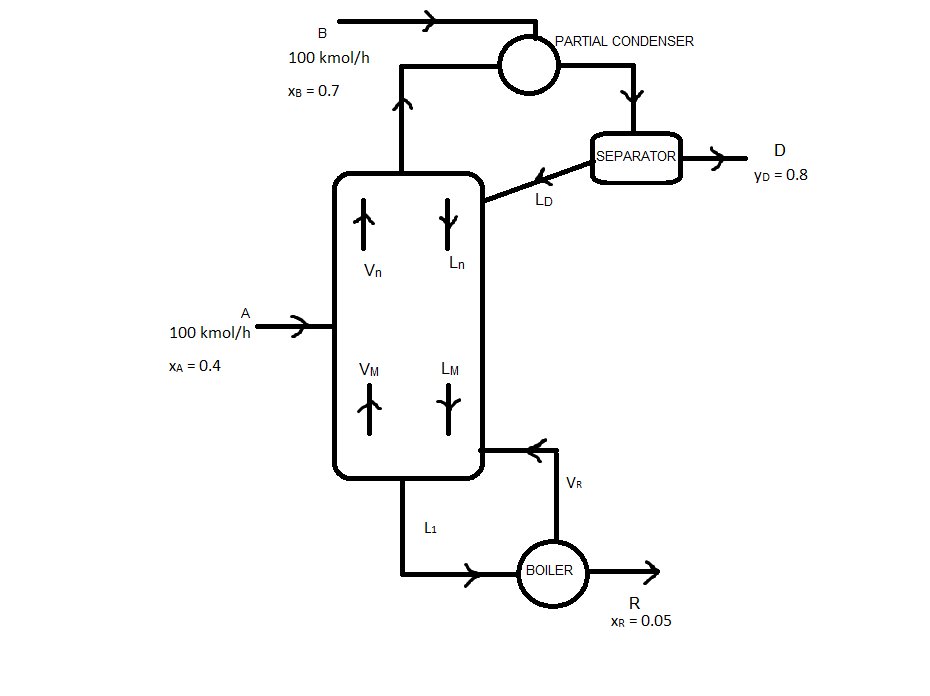
To the upper distillation column, it is fed onto the partial condenser 100 kmol/h (courrent B ) of a mixture that has 70% (in moles) of the compound we are interested in. To the propper column, it is also fed 100 kmol/h (courrent A) of the same mixture, with 40% (in moles) of the same compound. We obtain a Residue with 5% in moles of that compound, and a Distilate of 80% in moles.
Consider that VR/R = 1.5 · VR/R)minimum
Consider too that qB = qA = qLD = qD = 1 and qR = qVR = 0
Consider as compound 1 the compound of interest
- Molar flows of distillate and residue
- Feed equations
- Net flows of the column
- Molar flows of both phases in the column sectors
- Operative equations
- Minimum number of plates
- Number of plates when used the specified value of VR/R
- Most efficient position for the feed A
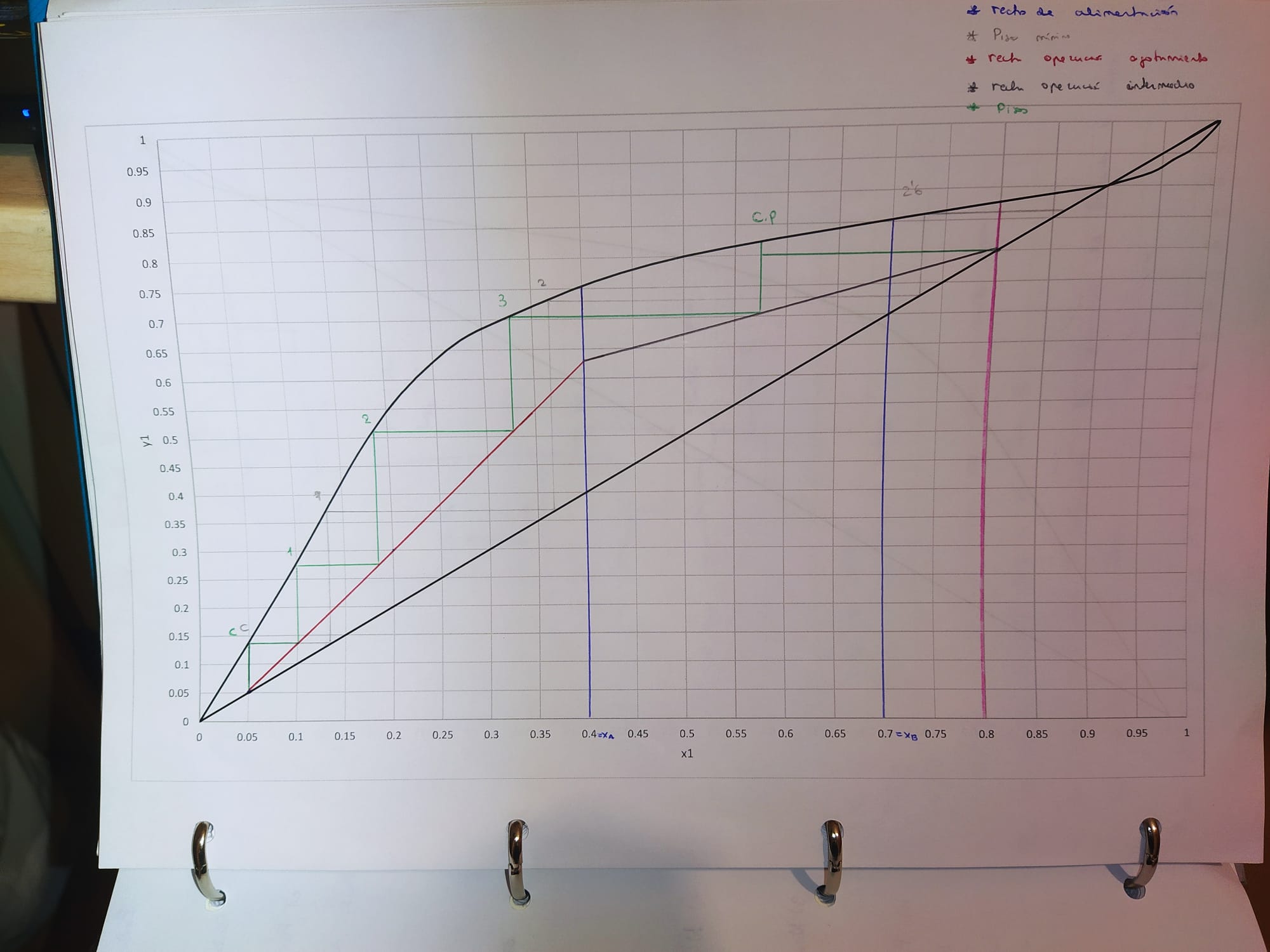
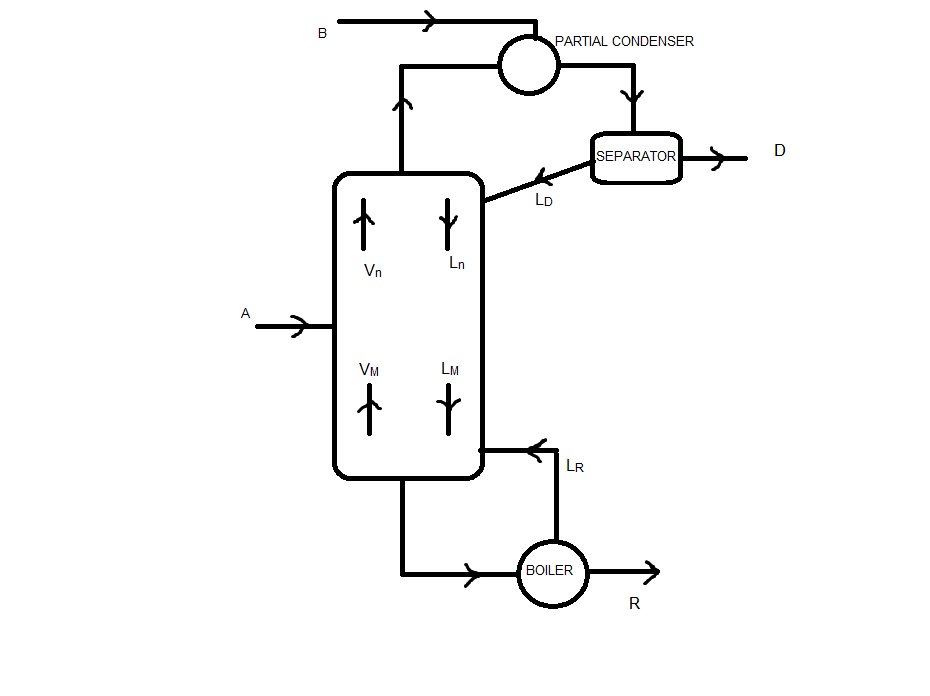
The diagram we will use is:
Okey so I proceede to explain the answers I've obtained:
- The molar flow of D and R
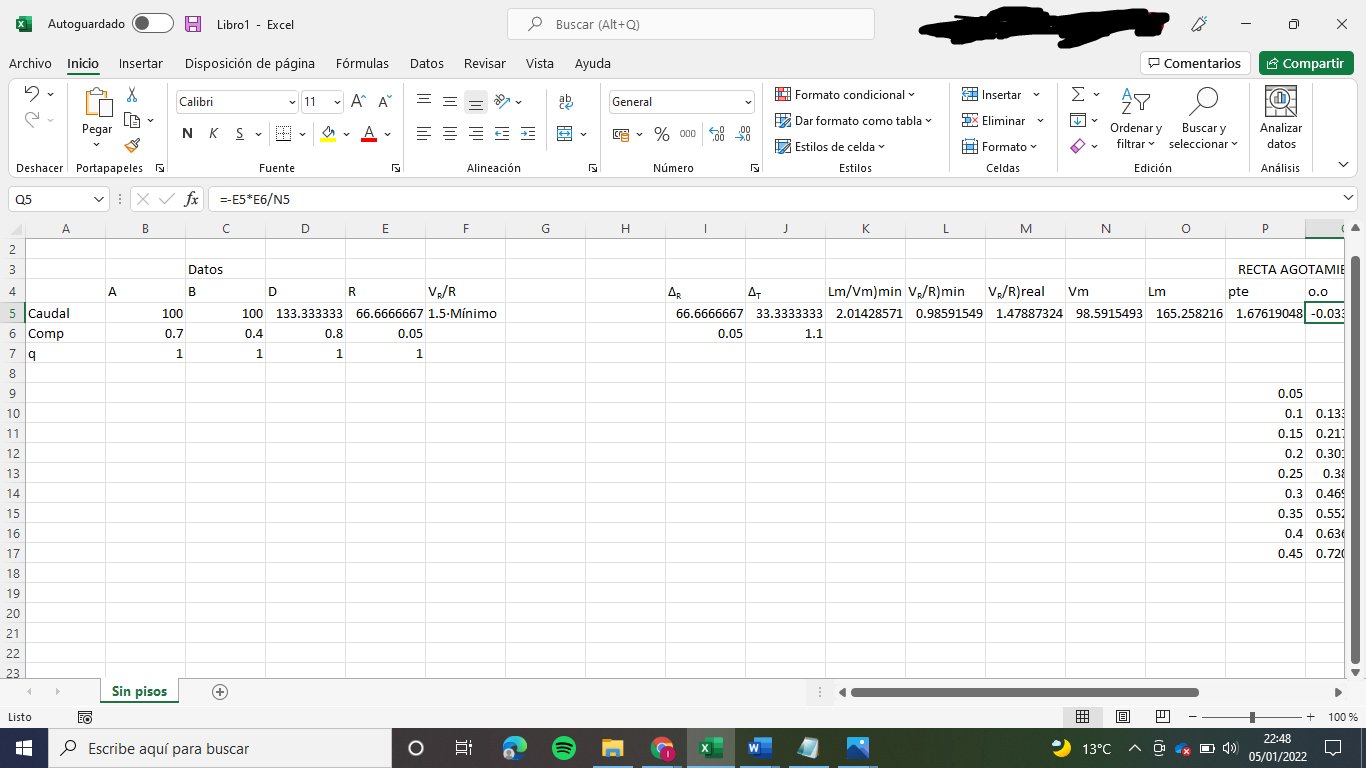
By making a mass balance we obtain two equations with two unknown variables (D and R)
A + B = D + R --> 100 + 100 = D + R
A·xA + B·xB = D·yD + R·xR --> 100·0.4 + 100·0.7 = D·0.8 + R·0.05
From here we obtain D and R
D = 133.33 kmol/h
R = 66.67 kmol/h
2. Feed equations
In general, the equation used to determine the equation of the feed is the following:
y = q/(q-1) · x - xA/(q-1)
As q = 1 for both A and B, the feed equations are:
A: y = 0.4
B: y = 0.7
3. Net flows of the column
Because we have a feed in the partial condenser, there is no net flow in the rectifying sector (I think)
So:
Stripping sector:
Lm - Vm = ΔR = R = 66.67 kmol/h
zΔR = xR = 0.05
Medium sector:
Mass balance: Ln + A = Vn + R
Vn - Ln = ΔT = A - R = 33.33 kmol/h
zΔT = (A·xA - R·xR)/ΔT = 1.10
4. Molar flows of both phases in the column
We have to determine firstly VR/R)min
We know that: Lm/Vm)max = (yΔR - yA,eq)/(xΔR - xA,eq)
yΔR = xΔR = 0.05
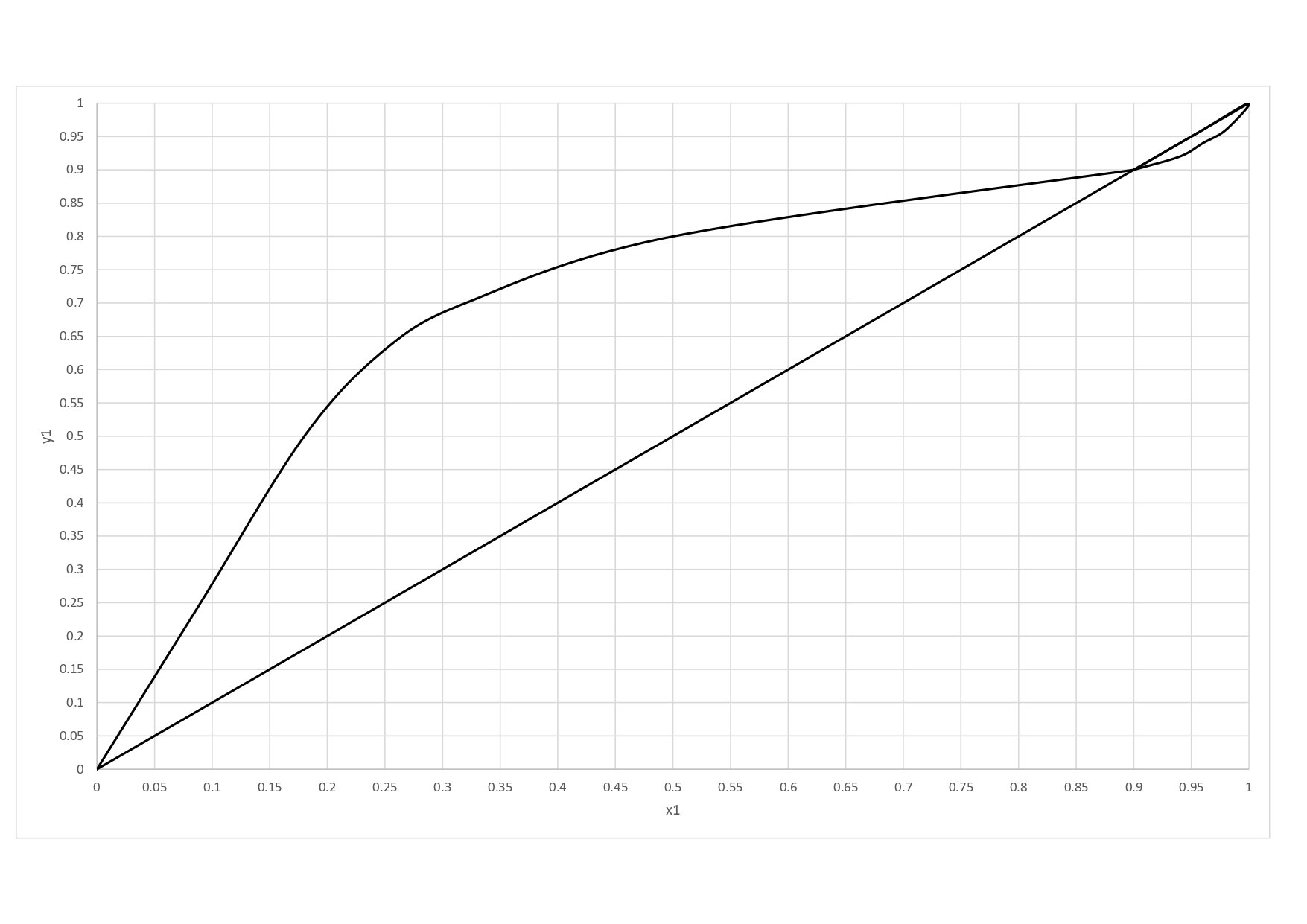
yA,eq is the point where the feed line cuts the equilibrium curve in the y x diagram, in this case: yA,eq = 0.755
xA,eq is the point where the feed line cuts the equilibrium curve in the y x diagram, in this case: xA,eq = 0.4
We obtain: Lm/Vm)max = 2.014
By a mass balance (i'm not going to make it because it would make the resolution too long) we know that:
Lm/Vm)max = (1+VR/R]min)/VR/R)min so we obtain:
VR/R)min = 0.986
As we know the relation between VR/R) = VR/R)min · 1.15 we obtain:
VR/R) = 1.47887
Now we can answer the question;
Stripping section:
Lm = Vm + R
We know that VR = Vm and that VR/R = Vm/R = 1.47887
so we can obtain Vm and consequently Lm:
Lm = 165.26 kmol/h
Vm = 98.59 kmol/h
We can calculate now the medium section:
Ln + Vm + A = Lm + Vn
Balance to the vapour: Vm + (1-qA)·A = Vn --> Vn = 98.59 kmol/h
Balance to the liquid: Ln + A·qA = Lm --> Ln = 65.26
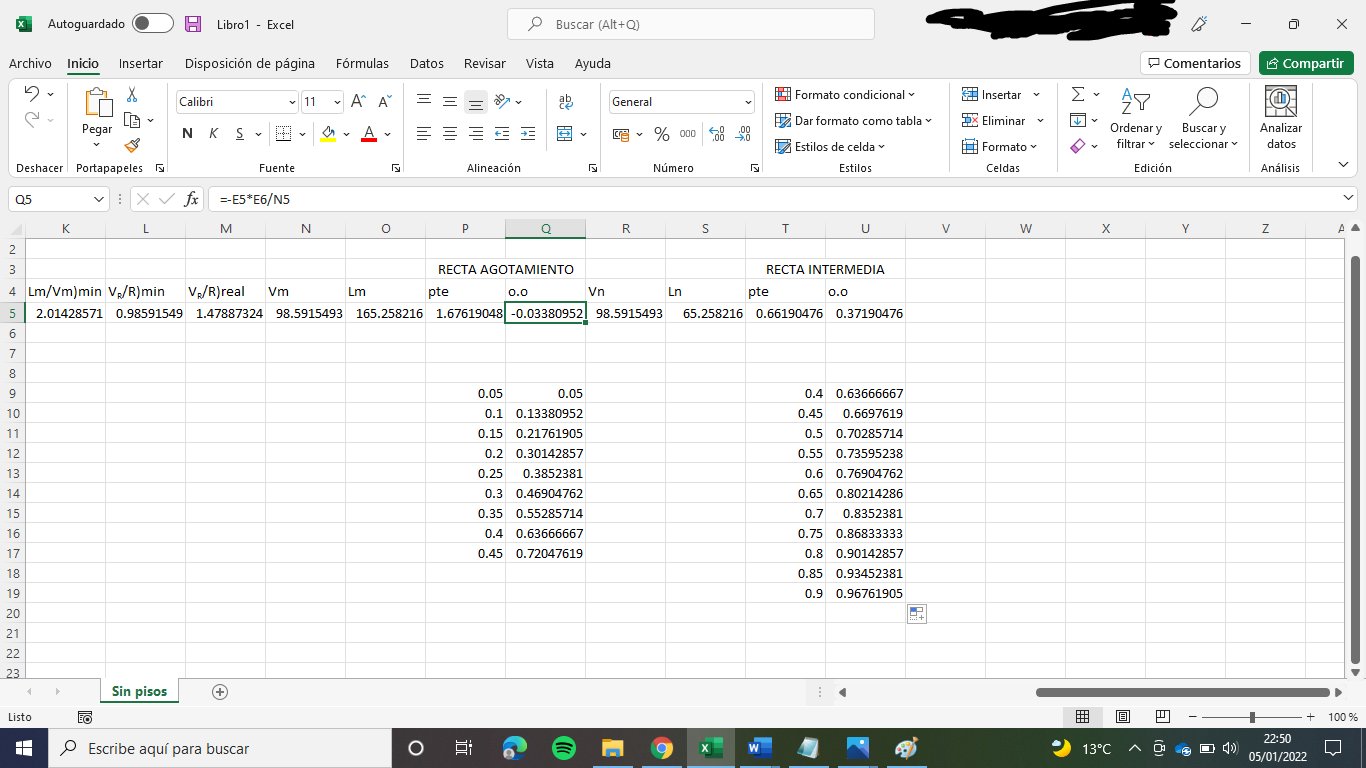
5. Operation lines:
Stripping operation line: ym = Lm/Vm· xm - R·xR/Vm
ym = 1.6762·xm - 0.0338
Medium section operation line: yn = Ln/Vn·xn + A·xA/Vn - R·xR/Vn
yn = 0.6619·xn + 0.3719
6. Minimum number of plates
3.6 - partial boiler - partial condenser --> 1.6 (see final image)
7. Number of plates
4.8 - partial boiler - partial condenser --> 2.8 (see final image)
8. Most efficient position of A
third plate counting from the bottom of the column
What do you think about it???


 FB
FB