Chemical and Process Engineering Resources

Centrifugal Pumps: Basic Concepts of Operation, Maintenance, and Troubleshooting
Nov 08 2010 11:30 AM | Mukesh Sahdev in Fluid Flow
Definition of Important Terms
The key performance parameters of centrifugal pumps are capacity, head, BHP (Brake horse power), BEP (Best efficiency point) and specific speed. The pump curves provide the operating window within which these parameters can be varied for satisfactory pump operation. The following parameters or terms are discussed in detail in this section.
Capacity
Head
- Significance of using Head instead of Pressure
- Pressure to Head Conversion formula
- Static Suction Head, hS
- Static Discharge Head, hd
- Friction Head, hf
- Vapor pressure Head, hvp
- Pressure Head, hp
- Velocity Head, hv
- Total Suction Head HS
- Total Discharge Head Hd
- Total Differential Head HT
NPSH
- Net Positive Suction Head Required NPSHr
- Net Positive Suction Head Available NPSHa
Power (Brake Horse Power, B.H.P) and Efficiency (Best Efficiency Point, B.E.P)
Specific Speed (Ns)
Affinity Laws
Capacity
Capacity means the flow rate with which liquid is moved or pushed by the pump to the desired point in the process. It is commonly measured in either gallons per minute (gpm) or cubic meters per hour (m3/hr). The capacity usually changes with the changes in operation of the process. For example, a boiler feed pump is an application that needs a constant pressure with varying capacities to meet a changing steam demand.
The capacity depends on a number of factors like:
- Process liquid characteristics i.e. density, viscosity
- Size of the pump and its inlet and outlet sections
- Impeller size
- Impeller rotational speed RPM
- Size and shape of cavities between the vanes
- Pump suction and discharge temperature and pressure conditions
For a pump with a particular impeller running at a certain speed in a liquid, the only items on the list above that can change the amount flowing through the pump are the pressures at the pump inlet and outlet. The effect on the flow through a pump by changing the outlet pressures is graphed on a pump curve.
As liquids are essentially incompressible, the capacity is directly related with the velocity of flow in the suction pipe. This relationship is as follows:
where: | Eq. (3) |
Head
Significance of Using the Term "Head" Instead of the Term "Pressure"
The pressure at any point in a liquid can be thought of as being caused by a vertical column of the liquid due to its weight. The height of this column is called the static head and is expressed in terms of feet of liquid.
The same head term is used to measure the kinetic energy created by the pump. In other words, head is a measurement of the height of a liquid column that the pump could create from the kinetic energy imparted to the liquid. Imagine a pipe shooting a jet of water straight up into the air, the height the water goes up would be the head.
The head is not equivalent to pressure. Head is a term that has units of a length or feet and pressure has units of force per unit area or pound per square inch. The main reason for using head instead of pressure to measure a centrifugal pump's energy is that the pressure from a pump will change if the specific gravity (weight) of the liquid changes, but the head will not change. Since any given centrifugal pump can move a lot of different fluids, with different specific gravities, it is simpler to discuss the pump's head and forget about the pressure.
So a centrifugal pump's performance on any Newtonian fluid, whether it's heavy (sulfuric acid) or light (gasoline) is described by using the term 'head'. The pump performance curves are mostly described in terms of head.
A given pump with a given impeller diameter and speed will raise a liquid to a certain height regardless of the weight of the liquid.Pressure to Head Conversion Formula
The static head corresponding to any specific pressure is dependent upon the weight of the liquid according to the following formula:
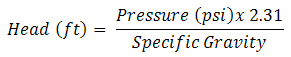 | Eq. (4) |
Newtonian liquids have specific gravities typically ranging from 0.5 (light, like light hydrocarbons) to 1.8 (heavy, like concentrated sulfuric acid). Water is a benchmark, having a specific gravity of 1.0.
This formula helps in converting pump gauge pressures to head for reading the pump curves.
The various head terms are discussed below.
Note: The Subscripts 's' refers to suction conditions and 'd' refers to discharge conditions.
- Static Suction Head, hS
- Static Discharge Head, hd
- Friction Head, hf
- Vapor pressure Head, hvp
- Pressure Head, hp
- Velocity Head, hv
- Total Suction Head HS
- Total Discharge Head Hd
- Total Differential Head HT
- Net Positive Suction Head Required NPSHr
- Net Positive Suction Head Available NPSHa
Static Suction Head (hs)
Head resulting from elevation of the liquid relative to the pump center line. If the liquid level is above pump centerline, hS is positive. If the liquid level is below pump centerline, hS is negative. Negative hS condition is commonly denoted as a "suction lift" condition.
Static Discharge Head, (hd)
It is the vertical distance in feet between the pump centerline and the point of free discharge or the surface of the liquid in the discharge tank.
Friction Head (hf)
The head required to overcome the resistance to flow in the pipe and fittings. It is dependent upon the size, condition and type of pipe, number and type of pipefittings, flow rate, and nature of the liquid.
Vapor Pressure Head (hvp)
Vapor pressure is the pressure at which a liquid and its vapor co-exist in equilibrium at a given temperature. The vapor pressure of liquid can be obtained from vapor pressure tables. When the vapor pressure is converted to head, it is referred to as vapor pressure head, hvp. The value of hvp of a liquid increases with the rising temperature and in effect, opposes the pressure on the liquid surface, the positive force that tends to cause liquid flow into the pump suction i.e. it reduces the suction pressure head.
Pressure Head (hp)
Pressure Head must be considered when a pumping system either begins or terminates in a tank which is under some pressure other than atmospheric. The pressure in such a tank must first be converted to feet of liquid. Denoted as hp, pressure head refers to absolute pressure on the surface of the liquid reservoir supplying the pump suction, converted to feet of head. If the system is open, hp equals atmospheric pressure head.
Velocity Head (hv)
Refers to the energy of a liquid as a result of its motion at some velocity 'v'. It is the equivalent head in feet through which the water would have to fall to acquire the same velocity, or in other words, the head necessary to accelerate the water. The velocity head is usually insignificant and can be ignored in most high head systems. However, it can be a large factor and must be considered in low head systems.
Total Suction Head (Hs)
The suction reservoir pressure head (hpS) plus the static suction head (hS) plus the velocity head at the pump suction flange (hVS) minus the friction head in the suction line (hfS).
| HS= hpS + hS + hvS - hfS | Eq. (5) |
The total suction head is the reading of the gauge on the suction flange, converted to feet of liquid.
Total Discharge Head (Hd)
The discharge reservoir pressure head (hpd) plus static discharge head (hd) plus the velocity head at the pump discharge flange (hvd) plus the total friction head in the discharge line (hfd).
| Hd= hpd + hd + hvd + hfd | Eq. (6) |
The total discharge head is the reading of a gauge at the discharge flange, converted to feet of liquid.
Total Differential Head (HT)
It is the total discharge head minus the total suction head or
| HT = Hd + HS (with a suction lift) | Eq. (7) |
| HT = Hd - HS (with a suction head) | Eq. (8) |

 FB
FB

17 Comments
Very help to all of them.
I think in Equation 9, fiction loss should be subtracted rather than being added, to get NPSHa.
could anyone tell me about 'hunting in pumps'??
very very nice article , its clear all concept about Pumps
good to understand.
Nice Article. Very helpful.
Appreciate that you are sharing your knowledge in such a fine manner. The content is so well presented that its very easy to follow.
Best,
Mayuresh.
Thanks for the article. Is there a similar article about compressor, heaters, or operation of columns (i,e stripper/frac)?
Thanks