Chemical and Process Engineering Resources

Centrifugal Pumps: Basic Concepts of Operation, Maintenance, and Troubleshooting
Nov 08 2010 11:30 AM | Mukesh Sahdev in Fluid Flow
NPSH
When discussing centrifugal pumps, the two most important head terms are NPSHr and NPSHa.
Net Positive Suction Head Required, NPSHr
NPSH is one of the most widely used and least understood terms associated with pumps. Understanding the significance of NPSH is very much essential during installation as well as operation of the pumps.
Pumps Can Only Pump Liquids, Not Vapor
The satisfactory operation of a pump requires that vaporization of the liquid being pumped does not occur at any condition of operation. This is so desired because when a liquid vaporizes its volume increases very much. For example, 1 ft3 of water at room temperature becomes 1700 ft3 of vapor at the same temperature. This makes it clear that if we are to pump a fluid effectively, it must be kept always in the liquid form.
Rise in temperature and fall in pressure induces vaporization
The vaporization begins when the vapor pressure of the liquid at the operating temperature equals the external system pressure, which, in an open system is always equal to atmospheric pressure. Any decrease in external pressure or rise in operating temperature can induce vaporization and the pump stops pumping. Thus, the pump always needs to have a sufficient amount of suction head present to prevent this vaporization at the lowest pressure point in the pump.
NPSH as a measure to prevent liquid vaporization
The manufacturer usually tests the pump with water at different capacities, created by throttling the suction side. When the first signs of vaporization induced cavitation occur, the suction pressure is noted (the term cavitation is discussed in detail later). This pressure is converted into the head. This head number is published on the pump curve and is referred as the "net positive suction head required (NPSHr) or sometimes in short as the NPSH. Thus the Net Positive Suction Head (NPSH) is the total head at the suction flange of the pump less the vapor pressure converted to fluid column height of the liquid.
NPSHr is a function of pump design
NPSH required is a function of the pump design and is determined based on actual pump test by the vendor. As the liquid passes from the pump suction to the eye of the impeller, the velocity increases and the pressure decreases. There are also pressure losses due to shock and turbulence as the liquid strikes the impeller. The centrifugal force of the impeller vanes further increases the velocity and decreases the pressure of the liquid. The NPSH required is the positive head in feet absolute required at the pump suction to overcome these pressure drops in the pump and maintain the majority of the liquid above its vapor pressure.
The NPSH is always positive since it is expressed in terms of absolute fluid column height. The term "Net" refers to the actual pressure head at the pump suction flange and not the static suction head.
NPSHr increases as capacity increases
The NPSH required varies with speed and capacity within any particular pump. The NPSH required increase as the capacity is increasing because the velocity of the liquid is increasing, and as anytime the velocity of a liquid goes up, the pressure or head comes down. Pump manufacturer's curves normally provide this information. The NPSH is independent of the fluid density as are all head terms.
Net Positive Suction Head Available, NPSHa
NPSHa is a function of system design
Net Positive Suction Head Available is a function of the system in which the pump operates. It is the excess pressure of the liquid in feet absolute over its vapor pressure as it arrives at the pump suction, to be sure that the pump selected does not cavitate. It is calculated based on system or process conditions.
NPSHa calculation
The formula for calculating the NPSHa is stated below:
NPSHas = hps + hs - hvps + hfs where: hps = Head pressure or the barometric pressure of the vessel converted to head | Eq. (9) |
NPSHa in a Nutshell
In a nutshell, NPSH available is defined as:
NPSHa = Pressure head + Static head - Vapor pressure head of your product - Friction head loss in the piping, valves and fittings. where all terms are in absolute feed of head. | Eq. (10) |
In an existing system, the NPSHa can also be approximated by a gauge on the pump suction using the formula:
NPSHa = hpS - hvpS ± hgS + hvS where: hpS = Barometric pressure in feet absolute | Eq. (11) |
Significance of NPSHr and NPSHa
The NPSH available must always be greater than the NPSH required for the pump to operate properly. It is normal practice to have at least 2 to 3 feet of extra NPSH available at the suction flange to avoid any problems at the duty point.
Power and Efficiency
Brake Horse Power (BHP)
The work performed by a pump is a function of the total head and the weight of the liquid pumped in a given time period. Pump input or brake horsepower (BHP) is the actual horsepower delivered to the pump shaft. Pump output or hydraulic or water horsepower (WHP) is the liquid horsepower delivered by the pump. These two terms are defined by the following formulas.
where: Q = Capacity in gallons per minute (GPM) | Eq. (12) |
where: Q = Capacity in gallons per minute (GPM) | Eq. (13) |
The constant 3960 is obtained by dividing the number or foot-pounds for one horsepower (33,000) by the weight of one gallon of water (8.33 pounds). BHP can also be read from the pump curves at any flow rate. Pump curves are based on a specific gravity of 1.0. Other liquids' specific gravity must be considered. The brake horsepower or input to a pump is greater than the hydraulic horsepower or output due to the mechanical and hydraulic losses incurred in the pump. Therefore the pump efficiency is the ratio of these two values.
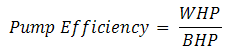 | Eq. (14) |
Best Efficiency Point (BEP)
The H, NPSHr, efficiency, and BHP all vary with flow rate, Q. Best Efficiency Point (BEP) is the capacity at maximum impeller diameter at which the efficiency is highest. All points to the right or left of BEP have a lower efficiency.
BEP as a measure of optimum energy conversion
When sizing and selecting centrifugal pumps for a given application the pump efficiency at design should be taken into consideration. The efficiency of centrifugal pumps is stated as a percentage and represents a unit of measure describing the change of centrifugal force (expressed as the velocity of the fluid) into pressure energy. The B.E.P. (best efficiency point) is the area on the curve where the change of velocity energy into pressure energy at a given gallon per minute is optimum; in essence, the point where the pump is most efficient.
BEP as a measure of mechanically stable operation
The impeller is subject to non-symmetrical forces when operating to the right or left of the BEP. These forces manifest themselves in many mechanically unstable conditions like vibration, excessive hydraulic thrust, temperature rise, and erosion and separation cavitation. Thus the operation of a centrifugal pump should not be outside the furthest left or right efficiency curves published by the manufacturer. Performance in these areas induces premature bearing and mechanical seal failures due to shaft deflection, and an increase in temperature of the process fluid in the pump casing causing seizure of close tolerance parts and cavitation.
BEP as an important parameter in calculations
BEP is an important parameter in that many parametric calculations such as specific speed, suction specific speed, hydrodynamic size, viscosity correction, head rise to shut-off, etc. are based on capacity at BEP. Many users prefer that pumps operate within 80% to 110% of BEP for optimum performance.
Specific Speed
Specific speed (Ns) is a non-dimensional design index that identifies the geometric similarity of pumps. It is used to classify pump impellers as to their type and proportions. Pumps of the same Ns but of different size are considered to be geometrically similar, one pump being a size-factor of the other.
Specific Speed Calculation
The following formula is used to determine specific speed:
where: Q = Capacity at best efficiency point (BEP) at maximum impeller diameter in gallons per minute (GPM) | Eq. (15) |
The understanding of this definition is of design engineering significance only, however, and specific speed should be thought of only as an index used to predict certain pump characteristics.
As per the above formula, it is defined as the speed in revolutions per minute at which a geometrically similar impeller would operate if it were of such a size as to deliver one gallon per minute flow against one-foot head.
Specific Speed as a Measure of the Shape or Class of the Impellers
The specific speed determines the general shape or class of the impellers. As the specific speed increases, the ratio of the impeller outlet diameter, D2, to the inlet or eye diameter, D1, decreases. This ratio becomes 1.0 for a true axial flow impeller. Radial flow impellers develop head principally through centrifugal force. Radial impellers are generally low flow high head designs. Pumps of higher specific speeds develop head partly by centrifugal force and partly by axial force. A higher specific speed indicates a pump design with head generation more by axial forces and less by centrifugal forces. An axial flow or propeller pump with a specific speed of 10,000 or greater generates its head exclusively through axial forces. Axial flow impellers are high flow low head designs.
Specific speed identifies the approximate acceptable ratio of the impeller eye diameter (D1) to the impeller maximum diameter (D2) in designing a good impeller.
Ns: 500 to 5000;D1/D2 > 1.5 -radial flow pump
Ns: 5000 to 10000;D1/D2 < 1.5 -mixed flow pump
Ns: 10000 to 15000; D1/D2 = 1 - axial flow pump
Specific speed is also used in designing a new pump by size-factoring a smaller pump of the same specific speed. The performance and construction of the smaller pump are used to predict the performance and model the construction of the new pump.
Suction Specific Speed (Nss)
Suction specific speed (Nss) is a dimensionless number or index that defines the suction characteristics of a pump. It is calculated from the same formula as Ns by substituting H by NPSHr.
In multi-stage pump the NPSHr is based on the first stage impeller NPSHR. Nss is commonly used as a basis for estimating the safe operating range of capacity for a pump. The higher the Nss is, the narrower is its safe operating range from its BEP. The numbers range between 3,000 and 20,000. Most users prefer that their pumps have Nss in the range of 8000 to 11000 for optimum and trouble-free operation.
The Affinity Laws
The Affinity Laws are mathematical expressions that define changes in pump capacity, head, and BHP when a change is made to pump speed, impeller diameter, or both. According to the Affinity Laws:
Capacity (Q) changes in direct proportion to impeller diameter D ratio, or to speed N ratio:
| Q2 = Q1 x [D2/D1] | Eq. (16) |
| Q2 = Q1 x [N2/N1] | Eq. (17) |
Head (H) changes in direct proportion to the square of impeller diameter D ratio, or the square of speed N ratio:
| H2 = H1 x [D2/D1]2 | Eq. (18) |
| H2 = H1 x [N2/N1]2 | Eq. (19) |
BHP changes in direct proportion to the cube of impeller diameter ratio, or the cube of speed ratio:
| BHP2 = BHP1 x [D2/D1]3 | Eq. (20) |
| BHP2 = BHP1 x [N2/N1]3 | Eq. (21) |
Where the subscript: 1 refers to initial condition, 2 refer to new condition.
If changes are made to both impeller diameter and pump speed the equations can be combined to:
| Q2 = Q1 x [(D2 x N2)/(D1 x N1)] | Eq. (22) |
H2 = H1 x [(D2 x N2)/(D1 x N1)]2 | Eq. (23) |
| BHP2 = BHP1 x [(D2 x N2)/(D1 x N1)]3 | Eq. (24) |
These equations are used to hand-calculate the impeller trim diameter from a given pump performance curve at a bigger diameter.
The Affinity Laws are valid only under conditions of constant efficiency

 FB
FB

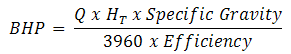
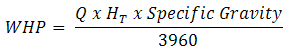
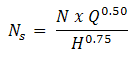
17 Comments
Very help to all of them.
I think in Equation 9, fiction loss should be subtracted rather than being added, to get NPSHa.
could anyone tell me about 'hunting in pumps'??
very very nice article , its clear all concept about Pumps
good to understand.
Nice Article. Very helpful.
Appreciate that you are sharing your knowledge in such a fine manner. The content is so well presented that its very easy to follow.
Best,
Mayuresh.
Thanks for the article. Is there a similar article about compressor, heaters, or operation of columns (i,e stripper/frac)?
Thanks