Chemical and Process Engineering Resources
Important Definitions
To enable a clear understanding of mechanism of cavitation, definitions of following important terms are explored:
- Static pressure
- Dynamic pressure
- Total pressure
- Static pressure head
- Velocity head
- Vapor pressure
Static Pressure (Ps)
The static pressure in a fluid stream is the normal force per unit area on a solid boundary moving with the fluid. It describes the difference between the pressure inside and outside a system, disregarding any motion in the system. For instance, when referring to an air duct, static pressure is the difference between the pressure inside the duct and outside the duct, disregarding any airflow inside the duct. In energy terms, the static pressure is a measure of the potential energy of the fluid.
Dynamic Pressure (Pd)
A moving fluid stream exerts a pressure higher than the static pressure due to the kinetic energy (½ mv2) of the fluid. This additional pressure is defined as the dynamic pressure. The dynamic pressure can be measured by converting the kinetic energy of the fluid stream into the potential energy. In other words, it is pressure that would exist in a fluid stream that has been decelerated from its velocity ‘v' to ‘zero' velocity.
Total Pressure (Pt)
The sum of static pressure and dynamic pressure is defined as the total pressure. It is a measure of total energy of the moving fluid stream. i.e. both potential and kinetic energy.
Relationship Between Ps, Pd, and Pt
In an incompressible flow, the relation between static, dynamic and total pressures can be found out using a simple device called Pitot tube (named after Henri Pitot in 1732) shown in Figure 1.
The Pitot tube has two tubes:
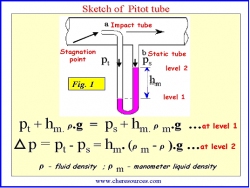 |
| Figure 1: Sketch of a Pilot Tube |
- Static tube (b'): The opening of the static tube is parallel to the direction of flow. It measures the static pressure, since there is no velocity component perpendicular to its opening.
- Impact tube (a): The opening of the impact tube is perpendicular to the flow direction. The point at the entrance of the impact tube is called as the stagnation point .At this point the kinetic energy of the fluid is converted to the potential energy. Thus, the impact tube measures the total pressure (also referred to as stagnation pressure) i.e. both static pressure and dynamic pressure (also referred to as impact pressure).
The two tubes are connected to the legs of a manometer or equivalent device for measuring pressure.
The relation between ps, pd and pt can be derived by applying a simple energy balance.
| Potential Energy + Kinetic Energy = Total Energy (Constant) | Eq. (1) |
As mentioned earlier, in the case of a fluid or gas the potential energy is represented by the static pressure and the kinetic energy by dynamic pressure. The kinetic energy is a function of the motion of the fluid, and of course it's mass. It is generally more convenient to use the density of the fluid (ρ) as the mass representation.
| K.E = pd = ½ m v2 = ½ρ v2 | Eq. (2) |
The corresponding pressure balance equation is:
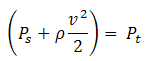 | Eq. (3) |
In place of the pressure terms as used above, it is more appropriate to speak of the energy during pumping as the energy per unit weight of the liquid pumped and the units of energy expressed this way are foot-pounds per pound (Newton-meters per Newton) or just feet (meters) i.e. the units of head. Thus the energy of the liquid at a given point in flow stream can be expressed in terms of head of liquid in feet.
The pressure term can be converted to head term by division with the factor ‘ρ g'. For unit inter-conversions the factor ‘ρ g/gc'. should be used in place of ‘ρg'.
Static Pressure Head
The head corresponding to the static pressure is called as the static pressure head.
 | Eq. (4) |
Velocity Head
The head corresponding to dynamic pressure is called the velocity head.
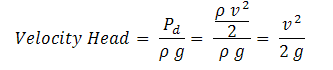 | Eq. (5) |
From the reading hmof the manometer velocity of flow can be calculated and thus velocity head can be calculated. The pressure difference, dP (Pt - Ps) indicated by the manometer is the dynamic pressure.
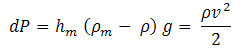 | Eq. (6) |
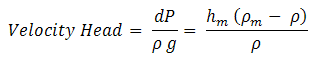 | Eq. (7) |
Vapor Pressure (Pv)
Vapor pressure is the pressure required to keep a liquid in a liquid state. If the pressure applied to the surface of the liquid is not enough to keep the molecules pretty close together, the molecules will be free to separate and roam around as a gas or vapor. The vapor pressure is dependent upon the temperature of the liquid. Higher the temperature, higher will be the vapor pressure.
Mechanism of Cavitation
The phenomenon of cavitation is a stepwise process as shown in Figure 2.
 |
| Figure 2: Steps in Cavitation |
The bubbles form inside the liquid when it vaporises i.e. phase change from liquid to vapor. But how does vaporization of the liquid occur during a pumping operation?
Vaporization of any liquid inside a closed container can occur if either pressure on the liquid surface decreases such that it becomes equal to or less than the liquid vapor pressure at the operating temperature, or the temperature of the liquid rises, raising the vapor pressure such that it becomes equal to or greater than the operating pressure at the liquid surface. For example, if water at room temperature (about 77 °F) is kept in a closed container and the system pressure is reduced to its vapor pressure (about 0.52 psia), the water quickly changes to a vapor. Also, if the operating pressure is to remain constant at about 0.52 psia and the temperature is allowed to rise above 77 °F, then the water quickly changes to a vapor.
Just like in a closed container, vaporization of the liquid can occur in centrifugal pumps when the local static pressure reduces below that of the vapor pressure of the liquid at the pumping temperature.
The vaporisation accomplished by addition of heat or the reduction of static pressure without dynamic action of the liquid is excluded from the definition of cavitation. For the purposes of this article, only pressure variations that cause cavitation shall be explored. Temperature changes must be considered only when dealing with systems that introduce or remove heat from the fluid being pumped.
 FB
FB


12 Comments
Great article but in your classification of pump problems, you have left out the most important class., i.e. problems in getting required parameters because of system conditions.Design Problems is of little use to the site engineer as he can't do anything about it. He can definitely correct system problems however.
Hii
I have a question regarding centrifugal pump.
A new pump is under commssioning in my plant and we have to go for water trial, can you please provide details on that how to proceed?
Great... thank u,,,,
THE BEST ONE...........
Thanks a lot ; it is much better than any other text about this topic in the pump literature , thanks again