Pressure Drop Of Pseudo-Plastic Fluids In Pipes

Dear All,
 
Pseudo-plastic fluids are a type of non-newtonian fluids and account for a majority of the non-newtonian fluids commonly found in the chemical process industry and specifically in the food processing industry.
 
Today's blog entry provides a methodology to calculate the pressure drop of a pseudo-plastic fluid in a pipe. An example problem is solved at the end of the outlined method. Readers can use the example problem to develop a spreadsheet based calculation
 
For Pseudo-plastic non-newtonian fluids, the power law model is used to define the shear stress versus velocity gradient relationship. The power law equation is as follows: 
 
τ = K*(dV/dy)^n
 
where:
τ = shear stress at distance y from pipe wall
K = flow consistency index
dV/dy = velocity gradient or shear rate
n = flow behavior index

For pseudo-plastic fluids n < 1, and for dilatant fluids n > 1. Since the apparent viscosity μ is the slope of the shear stress τ versus velocity gradient plot, we can calculate the apparent viscosity of a non-newtonian fluid that follows the power law from the following equation
 
µ =K*(dV/dy)^n-1
 
or 
K = 0.001*µ*(dV/dy)^1-n
 
where:
µ = Apparent Viscosity, cP
K = Flow consistency index, Pa.sⁿ
dV/dy = velocity gradient, s^-1
n = flow behavior index, dimensionless
 
Power-Law Reynolds Number:
 
Re_PL = 2^3-n*(n / (3n+1))ⁿ*((V^2-n*Dⁿ*ρ) / K)
 
where:
Re_PL = Power-Law Reynolds Number, dimensionless
V = Velocity of flow in pipe, m/s
D = Inside diameter of pipe, m
ρ = density of the fluid, kg/m³
 
Determining fanning friction factor 'f' for laminar flow of power-law fluids:
 
f = 16 / Re_PL
 
where:
f = fanning friction factor, dimensionless
 
Note:
The transition from Laminar to Turbulent flow for pseudo-plastic fluids is considered at a Reynolds number of 2100.
 
Determining fanning friction factor 'f' for turbulent flow of power-law fluids:
 
Refer attached chart
 

 
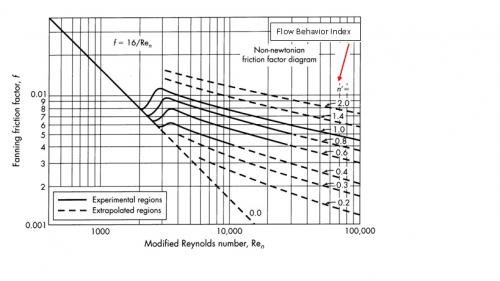
Friction Loss (in head) using Fanning friction factor:
 
h_f = 2*f*V²*L / (g*d)
where:
h_f = friction loss (in head) in the pipe, m (meters of liquid column)
L = Length of the pipe, m
g = Acceleration due to gravity, 9.81 m/s²
 
Example Problem:
 
A coal slurry is to be transported by horizontal pipeline. It has been determined that the slurry may be described by the power law model with a flow behavior index of 0.4, an apparent viscosity of 50 cP at a shear rate of 100 /s, and a density of 1442 kg/m³. What would be the pressure drop and the horsepower (HP) required to pump the slurry at a rate of 0.06 m³/s through an 8 in. Schedule 40 pipe that is 80 km long ?
 
Inputs:
 
n = 0.4
µ = 50 cP
dV/dy = 100 s^-1
ρ = 1442 kg/m³
D = 0.202 m (based on nominal pipe size in inches and Pipe schedule)
L = 80 km
Q = 0.06 m³/s
 
Results:
L = 80,000 m
K = 0.792 Pa.sⁿ
V = 1.87 m/s
Re_PL = 8025
f = 0.0048 (from chart)
h_f = 1358 m
ΔP = 192 bar
HP = 1153038 W = 1153 kW
 
Hope all of you have found this blog entry very informative. I look forward to comments from the readers of my blog.
 
Regards,
Ankur.