Search Results
By content type
By section
-
Flow Through Orifice Plates in Compressible Flu...
The calculation of compressible flow through orifice plates at high dP (critical flow) appears to be carried out incorrectly in most instances. This flow condition is often encountered on gas plants, compressor stations and pipelines where orifice plates are commonly used as a cheap and convenient way to regulate blowdown and pressurising rates. Blowdown must be achieved within the time period required to make the plant safe but at the same time without an excessive rate of pressure drop that could damage equipment. A more accurate calculation method is proposed below and should be used to improve the engineering predictions.
Orifice flow calculations typically use the following equations or some variant of them:
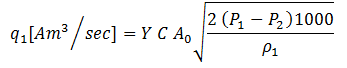
Crane Eq. 2-24 / Eq. (1)
Where subscript "1" indicates upstream conditions, subscript "2" indicates downstream conditions and Ao is the orifice cross section area.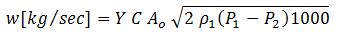
Crane Eq. 2-23 / Eq. (2) Download this calculator in our Online Store
For metering applications the ASME equation is often used to determine the Expansion Factor Y:
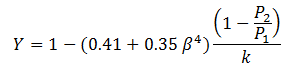
Eq. (3) for flange taps, where P and T are in absolute units.
For high accuracy metering (e.g. AGA 3) use of these calculations is often limited to
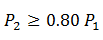 .
.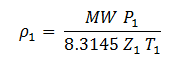
Eq. (4) where P and T are in absolute units.
It is then often assumed that the orifice flow goes critical (i.e. sonic velocity) at P2 = 0.528 x P1 (for air) and the choked flow equation is then applied:
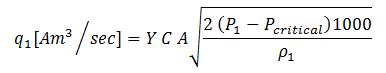
Eq. (5) 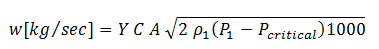
Eq. (6) (Crane Pg 2-15), where Pcr = 0.528 x P1
For P2 less than Pcr this method assumes that the flow does not increase further.
Download additional information on the derivation of this method in our Article Supplements Repository
- Oct 16 2012 12:40 PM
- by dkirk
-
Understanding Compressible Flow
Understanding the flow of compressible fluids in pipes is necessary for a robust design of process plants. The main difference between incompressible fluid, like water, and compressible fluid, vapor, is the greater change in pressure and density. This makes the calculations for compressible fluids slightly more difficult. Understanding how the fluid properties change is critical when dealing with these fluids. The ability of compressible fluids, unlike incompressible fluids, to "choke" further complicates matters.
{parse block="google_articles"}Practical applications of this topic include sizing relief valve outlet laterals and low-pressure compressor suction lines. These pose a special challenge as the velocities and pressure changes are high.
Adiabatic Flow of a Compressible Fluid Through a Conduit
Flow through pipes in a typical plant where line lengths are short, or the pipe is well insulated can be considered adiabatic. A typical situation is a pipe into which gas enters at a given pressure and temperature and flows at a rate determined by the length and diameter of the pipe and downstream pressure. As the line gets longer friction losses increase and the following occurs:
- Pressure decreases
- Density decreases
- Velocity increases
- Enthalpy decreases
- Entropy increases
The question is "will the velocity continue to increasing until it crosses the sonic barrier?" The answer is NO. The maximum velocity always occurs at the end of the pipe and continues to increase as the pressure drops until reaching Mach 1. The velocity cannot cross the sonic barrier in adiabatic flow through a conduit of constant cross section. If an effort is made to decrease downstream pressure further, the velocity, pressure, temperature and density remain constant at the end of the pipe corresponding to Mach 1 conditions. The excess pressure drop is dissipated by shock waves at the pipe exit due to sudden expansion. If the line length is increased to drop the pressure further the mass flux decreases, so that Mach 1 is maintained at the end of the pipe.
Analyzing the adiabatic flow using energy and mass balance yields the following analyses along with this nomenclature:
Table 1: Nomenclature Variable Definition Variable Definition h enthalpy/unit mass hst stagnation enthalpy v velocity Ma Mach number g gravitational constant M molecular weight z elevation T temperature Q heat flow P pressure Ws shaft work R gas constant Cp specific heat (constant pressure) Z compressibility r density g Cp/Cv G mass flux  Â
- May 31 2012 10:16 AM
- by rxnarang

 FB
FB

